Eigenschaften von Binomialverteilungen erkunden

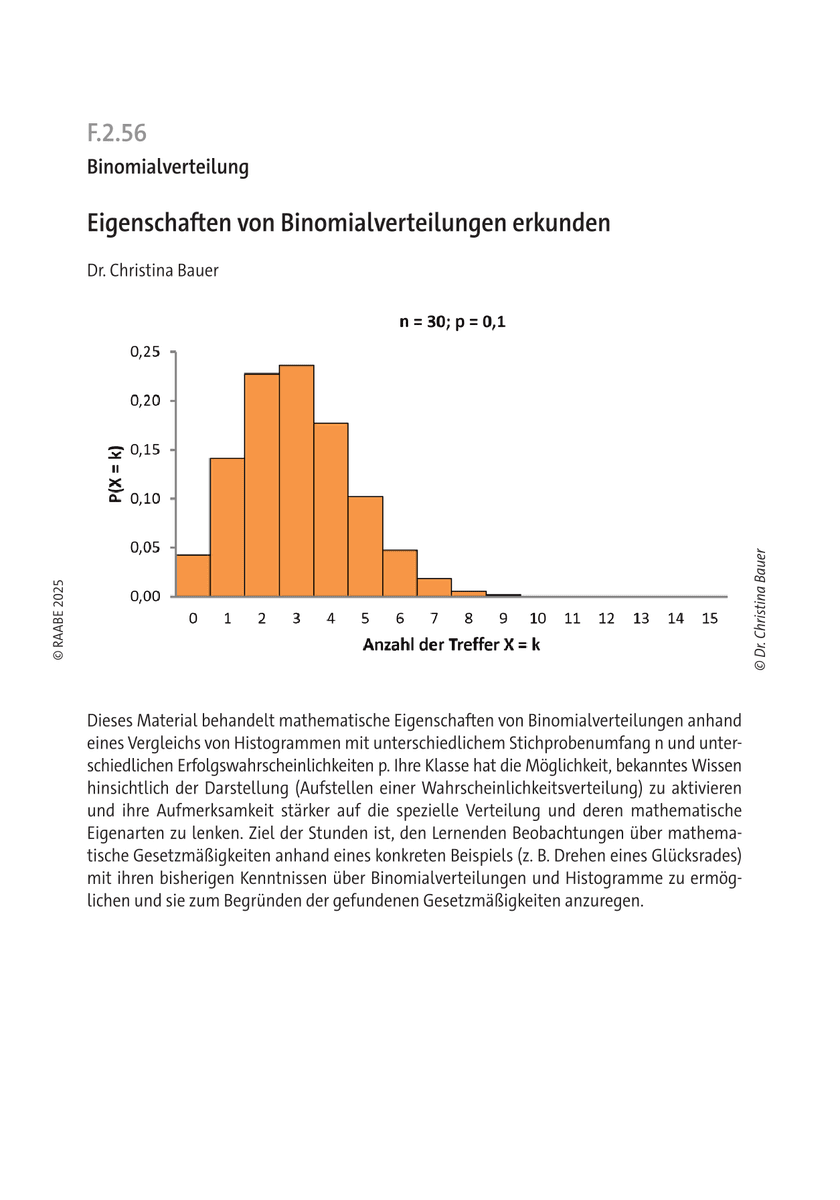
Dieses Material behandelt mathematische Eigenschaften von Binomialverteilungen anhand eines Vergleichs von Histogrammen mit unterschiedlichem Stichprobenumfang n und unterschiedlichen Erfolgswahrscheinlichkeiten p. Ihre Klasse hat die Möglichkeit, bekanntes Wissen hinsichtlich der Darstellung (Aufstellen einer Wahrscheinlichkeitsverteilung) zu aktivieren und ihre Aufmerksamkeit stärker auf die spezielle Verteilung und deren mathematische Eigenarten zu lenken. Ziel der Stunden ist, den Lernenden Beobachtungen über mathematische Gesetzmäßigkeiten anhand eines konkreten Beispiels (z. B. Drehen eines Glücksrades) mit ihren bisherigen Kenntnissen über Binomialverteilungen und Histogramme zu ermöglichen und sie zum Begründen der gefundenen Gesetzmäßigkeiten anzuregen.